若是中国古人早发明了变量，那很多定理估计都要以中国人命名了。

比较著名的定理有勾股定理和孙子定理，但是勾股定理西方也不大承认，认为勾三股四弦五这句话未经证明，取而代之的是毕达哥拉斯定理。只有孙子定理还是颇受认可的。

《孙子算经》中是这么说的：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

《孙子歌》中有详细的解决方法

三人同行七十希，五樹梅花廿一支，七子團圓正半月，除百零五使得知。

以上解法若推廣到一般情況，便得到了中國剩餘定理的一個構造性證明。

一般地，中國剩餘定理是指若有一些两两互质的整数 ，则对任意的整数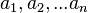：，以下联立同餘方程组对模  有公解：

 

大概解决方法就是对于m_i，i=1,2...n，求其它m_k，k!=i的公倍数中除以m_i余1的最小，得到n个这样的满足条件的最小公倍数，然后分别乘以对应的a_k,最后相加， 再减去a_1，a_2...a_n的最小公倍数的倍数，得到的最小正数即为符合要求的最小解。

孙子老祖实在是厉害，上面的解法也是优化过的，不求余数位a1，但求余数为1，再乘以a1，这样满足要求了